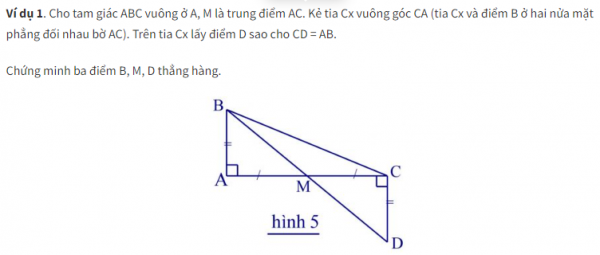
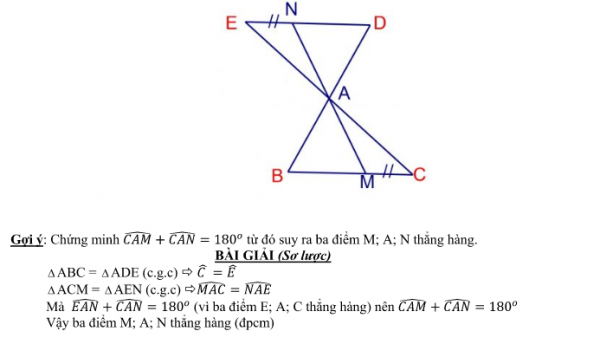
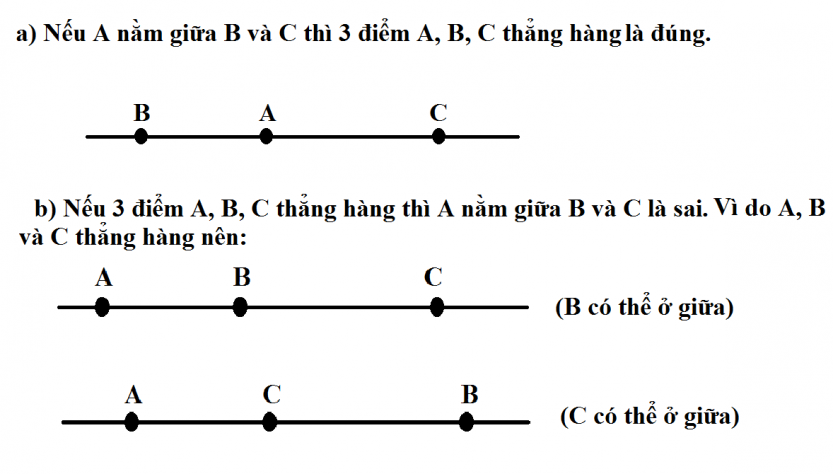
Cách chứng minh 3 điểm thẳng hàng là dạng toán luôn có trong các đề thi vào lớp 10, Bài viết này svnckh sẽ giới thiệu đến các bạn các phương pháp và cách giải để chứng minh 3 điểm thẳng hàng kèm theo đó dưới bài viết bao gồm bài tập và lời giải chi tiết. Mời các bạn cùng theo dõi.
3 điểm thẳng hàng là gì?
Ba điểm thẳng hàng khi chúng cùng thuộc một đường thẳng.
Xem thêm : Định nghĩa đường thẳng là gì?
Quan hệ của 3 điểm thẳng hàng
3 điểm thẳng hàng thì 3 điểm đó phân biệt và cùng nằm trên một đường thẳng.
Chỉ có một và chỉ một điểm nằm giữa hai điểm còn lại trong ba điểm thẳng hàng.
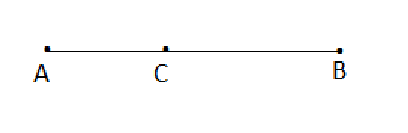
Phương pháp chứng minh 3 điểm thẳng hàng
1. Sử dụng hai góc kề bù có ba điểm nằm trên hai cạnh là hai tia đối nhau.
2. Ba điểm cùng thuộc một tia hoặc một một đường thẳng
3. Trong ba đoạn thẳng nối hai trong ba điểm có một đoạn thẳng bằng tổng hai đoạn thẳng kia.
4. Hai đoạn thẳng cùng đi qua hai trong ba điểm ấy cùng song song với đường thẳng thứ ba.
5. Hai đường thẳng cùng đi qua hai trong ba điểm ấy cùng vuông góc với đường thẳng thứ ba.
6. Đường thẳng cùng đi qua hai trong ba điểm ấy có chứa điểm thứ ba.
7. Sử dụng tính chất đường phân giác của một góc, tính chất đường trung trực của đoạn thẳng, tính chất ba đường cao trong tam giác
8. Sử dụng tính chất hình bình hành.
9. Sử dụng tính chất góc nội tiếp đường tròn.
10. Sử dụng góc bằng nhau đối đỉnh
11. Sử dụng trung điểm các cạnh bên, các đường chéo của hình thang thẳng hàng
12. Chứng minh phản chứng
13. Sử dụng diện tích tam giác tạo bởi ba điểm bằng 0
14. Sử dụng sự đồng qui của các đường thẳng.
Xem thêm : Đoạn thẳng là gì?
Các cách chứng minh ba điểm thẳng hàng
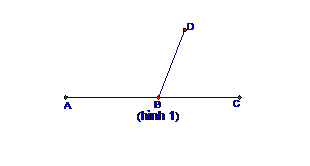
Phương pháp 1:
Nếu ∠ABD + ∠DBC = 180o thì ba điểm A; B; C thẳng hàng.
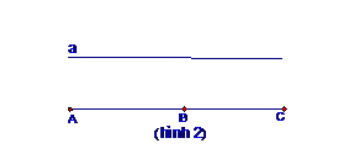
Phương pháp 2 :
Nếu AB // a và AC // a thì ba điểm A; B; C thẳng hàng.
(Cơ sở của phương pháp này là: tiên đề Ơ – Clit- tiết 8- hình học lớp 7)
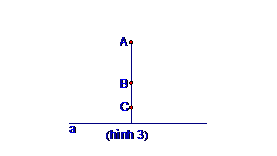
Phương pháp 3:
Nếu AB ⊥ a; AC ⊥ a thì ba điểm A; B; C thẳng hàng.
(Cơ sở của phương pháp này là: Có một và chỉ một đường thẳng a’ đi qua điểm O và vuông góc với đường thẳng a cho trước)
Hoặc A; B; C cùng thuộc một đường trung trực của một đoạn thẳng .(tiết 3- hình học lớp 7)
Phương pháp 4 :
Nếu tia OA và tia OB là hai tia phân giác của góc xOy thì ba điểm O; A; B thẳng hàng.
Cơ sở của phương pháp này là: Mỗi góc có một và chỉ một tia phân giác .
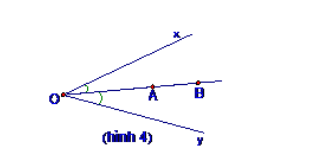
* Hoặc : Hai tia OA và OB cùng nằm trên nửa mặt phẳng bờ chứa tia Ox, ∠xOA = ∠xOB thì ba điểm O, A, B thẳng hàng.
Phương pháp 5:
Nếu K là trung điểm BD, K’ là giao điểm của BD và AC. Nếu K’ là trung điểm BD và K’ ≡ K thì A, K, C thẳng hàng.
(Cơ sở của phương pháp này: Mỗi đoạn thẳng chỉ có một trung điểm)
Bài tập